Register Class

A Sandcastle Documented Class Library

The basic unit needed for performing quantum computation.

Remarks

QuantumComputer may have zero to many Registers, but at least one is required to perform quantum computations. Register consist of qubits, which are targets for quantum gates. To apply a quantum gate, use methods of Register class (for computation on its qubits) or extension methods of QuantumComputer class (for computation on qubits in different registers; see Quantum.Operations).

Inheritance Hierarchy

System Object
Quantum Register

Namespace: Quantum
Assembly: Quantum (in Quantum.dll) Version: 1.0.0.0 (1.0.0.0)

Syntax

C++

Copy to Clipboard Print

public class Register : IRegister

public class Register : IRegister

The Register type exposes the following members.

Methods

	Name	Description
	CNot	Performs a controlled not operation (C-NOT Gate). The target bit gets inverted if the control bit is enabled. The operation can be written as the unitary operation matrix: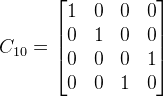
	CPhaseShift	Performs a conditional phase kick (or phase shift) on the register's state by the angle PI / 2 ^ dist. The operation is represented by the unitary matrix: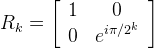
	Equals	Determines whether the specified object is equal to the current object. (Inherited from Object.)
	Finalize	Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.)
	Gate1	Performs any arbitrary unitary operation on target qubit. The operation is described by unitary matrix of complex numbers, as follows:
	GetAmplitudes	Returns amplitudes of each possible state of register. Amplitude is a complex number, which squared magnitude is the probability of the state. If register is entangled, the amplitudes cannot be computed. Thus, the method GetAmplitudes() returns null for such registers. The method returns meaningful value, if register is RootRegister, or if it was not a part of multi-register operations (see Quantum.Operations). Even if the register is not entangled with any other, but was used in multi-register operation, the returned value is null because such operation connect participating registers into one RootRegister.
	GetHashCode	Serves as a hash function for a particular type. (Inherited from Object.)
	GetProbabilities	Returns probabilities of each possible state of register. It means that after measurement register remains in particular state with corresponding probability.
	GetType	Gets the Type of the current instance. (Inherited from Object.)
	GetValue	Returns the integer value stored in register, if there is only one possibility. If the register is a superposition of multiple states, the method returns null.
	GetVector	Returns a vector of amplitudes of each possible state. If register is a part of other register, this method returns null (see GetAmplitudes(Register)).
	Hadamard	Applies the Hadamard gate to the target qubit. The unitary matrix for this operation is: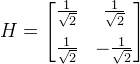
	InverseCPhaseShift	Performs a inversed conditional phase kick (or phase shift) on the register's state by the angle PI / 2 ^ dist. The operation is represented by the unitary matrix: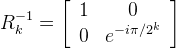
	Measure	Performs measurement of whole register.
	Measure(Int32)	Performs measurement of single qubit in register. After measurement, the width of the register remains the same.
	MemberwiseClone	Creates a shallow copy of the current Object. (Inherited from Object.)
	PhaseKick	Performs a phase kick (or phase shift) on the the register's state. The operation is represented by the unitary matrix: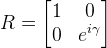
	PhaseScale	Adds a global phase on the register's state. The operation is represented by the unitary matrix: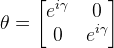
	Reset
	RotateX	Performs a rotation of the target qubit about the x-axis of the Bloch sphere. The angle of rotation is given in first argument (double gamma). The unitary matrix of this operation is: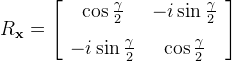
	RotateY	Performs a rotation of the target qubit about the y-axis of the Bloch sphere. The angle of rotation is given in first argument (double gamma). The operation is represented by the unitary matrix: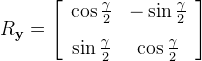
	RotateZ	Performs a rotation of the target qubit about the z-axis of the Bloch sphere. The angle of rotation is given in first argument (double gamma). The operation is represented by the unitary matrix: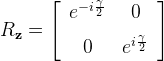
	SigmaX	Performs a Sigma X Pauli's Gate on target qubit. Actually, it is a simple Not. The unitary operation matrix is: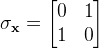
	SigmaY	Performs a Sigma Y Pauli's Gate on target qubit. The operation is represented by unitary matrix: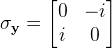
	SigmaZ	Performs a Sigma Z Pauli's Gate on target qubit. The operation is represented by unitary matrix: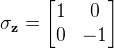
	SqrtX	Performs the Square Root of Not on the target qubit. The Square Root of Not Gate is such a gate, that applied twice, performs Not operation. The operation can be represented as the unitary matrix: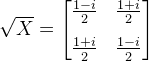
	Toffoli	Applies Toffoli gate. If all of the control bits are enabled, the target bit gets inverted. This gate with more than two control bits is not considered elementary and is not available on all physical realizations of a quantum computer. Toffoli gate with two control bits can be represented by unitary matrix: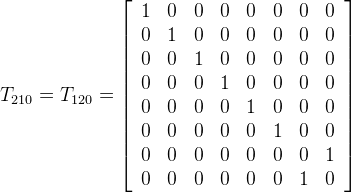
	ToString	Overrides native ToString() method, for friendly printing Register's content. (Overrides Object ToString .)

Top

Operators

	Name	Description
	(Register to RegisterRef)	For completeness. The Register could be implicitly casted to the reference to its first qubit. Like in arrays, where an address of an array is also the address of its first element.

Top

Properties

	Name	Description
	Item Int32	Returns reference to single qubit in register.
	Item Int32, Int32	Returns a sub-register, which begins at given offset and has given width.
	OffsetToRoot	Right after creation, register is independent and its OffsetToRoot equals 0. But after operations on many registers, included this, Register could be entangled with others and is no longer independent. The group of entangled registers has its RootRegister. Each register in such group is de facto a part of the Root. OffsetToRoot describes offset (from Least Significant Bit, which offset is 0) of the part in RootRegister.
	Width	The number of qubits contained in Register.

Top